Especial Tabuada
Curso para professores de 1º ao 5º ano do Ensino Fundamental. Matemática 1 (multiplicação).
A adição de parcelas iguais
- Uma caixa de lápis de cor contém 6 lápis. Quantos lápis há em 3 caixas iguais a essa?
Situações como essa que descrevemos explicam por que, atualmente, a maioria das professoras começa a ensinar a multiplicação de parcelas iguais. Elas explicam ás crianças que 3 x 6 significa 6 + 6 + 6, que 2 x 5significa 5 + 5, e assim por diante.
A multiplicação pode ser considerada como uma maneira abreviada de indicar a adição de parcelas iguais. Essa idéia de adição de parcelas iguais aparece em várias situações, como, por exemplo, a organização retangular.
A organização retangular
Considere estes problemas:
- Márcio, o marceneiro, fez um armário cheio de gavetas. Veja:
Quantas são as gavetas?
- Jurandir já assentou a primeira fileira e a primeira coluna de azulejos na parede da cozinha. Veja:
Quantos azulejos serão gastos para revestir a parede toda?
Os dois problemas podem, no entanto, ser resolvidos com o uso da multiplicação.
Como há 7 fileiras de gavetas, o total é:
Cada fileira tem 22 azulejos; são 12 fileiras; total de azuleijos: 12 x 22 = 264
Nesta figura, pode-se encontrar o total de quadradinhos fazendo 3 x 6 = 18, pois temos 6 fileiras de 6.Mas também é correto encontrar o total fazendo 6 x 3 = 18, pois há 6 colunas de 3.
A área do quadrado de lado 4 é igual a 4 x 4, pois no seu interior cabem 4 x 4 quadradinhos unitários.
A área do retângulo de lados 3 e 5 é igual a 3 x 5 (ou 5 x 3), pois este é o número de quadradinhos unitários que cabem em seu interior.
A área desta figura é igual a 31 porque cabem 31 quadradinhos unitários no seu interior.
3 + 3 + 3 + 3 ou 4 x 3ou 4 + 4 + 4 ou 3 x 4 ou ...
2 + 2 + 2 + 2 + 2 ou 5 x 2ou 5 + 5 ou 2 x 5 ou ...
3 + 3 + 3 + 6 + 6ou 3 x 3 + 2 x 6
ou 2 + 2 + 2 + 5 + 5 + 5
ou 3 x 2 + 3 x 5 ou ...
No próximo matemática das séries iniciais 2, falaremos sobre O raciocínio combinatório. Que faz parte do processo de compreensão da multiplicação. Te espero, até lá.
Este curso foi desenvolvido e projetado por professores e alunos do ICMC/USP. O curso pode ser realizado por qualquer usuário que tenha acesso à Internet e é inteiramente gratuito.
Fonte: http://educar.sc.usp.br/matematica/matematica.html
http://ideiacriativaensinofundamental1.blogspot.com/2011/07/tabuada-divertida-multiplicacao-1-9.html
LINK COM JOGOS
http://matematicanaredi.blogspot.com/2009/08/jogos-multiplicacao.html ______ 3 º ano
Links com atividades:
http://pedagogiaseculoxxi.blogspot.com/2011/03/atividades-tabuada.html
http://pedagogiaseculoxxi.blogspot.com/2011/01/matematica-multiplicacao.html
http://pedagogiaseculoxxi.blogspot.com/2011/01/matematica-atividades-com-operacoes.html
http://revistaguiafundamental.uol.com.br/professores-atividades/80/imprime191844.asp
http://pedagogiaseculoxxi.blogspot.com/2011/01/matematica-multiplicacao.html
http://pedagogiaseculoxxi.blogspot.com/2011/01/matematica-atividades-com-operacoes.html
http://revistaguiafundamental.uol.com.br/professores-atividades/80/imprime191844.asp
ESPECIAL TABUADA - PARTE 2
Tabuada do 3
Agora Complete:
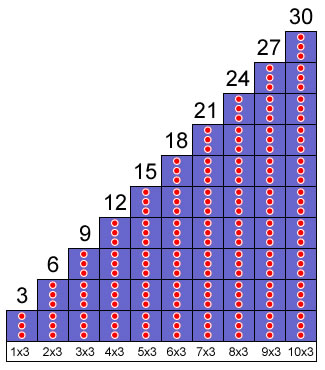
| a) 1 vezes 3 é igual a | e) 5 vezes 3 é igual a |
| b) 2 vezes 3 é igual a | f) 6 vezes 3 é igual a |
| c) 3 vezes 3 é igual a | g) 7 vezes 3 é igual a |
| d) 4 vezes 3 é igual a | h) 8 vezes 3 é igual a |
| i) 9 vezes 3 é igual a | j) 10 vezes 3 é igual a |
a) x 3 = 30
b) x 3 = 15
c) x 3 = 6
d) x 3 = 24
e) x 3 = 0
f) x 3 = 9
g) x 3 = 27
h) x 3 = 3
i) x 3 = 21
j) x 3 = 12
3) Vamos colocar o sinal de + ou de x, de acordo com o resultado:
a) 3 2 = 6
b) 3 5 = 8
c) 3 9 = 12
d) 3 9 = 27
e) 3 7 = 10
f) 3 5 = 15
g) 3 1 = 3
h) 3 3 = 6
i) 3 4 = 12
j) 3 6 = 9
l) 3 2 = 5
m)3 8 = 24
4) Nas fichas estão indicadas as multiplicações:
8 x 3
|
5 x 3
|
a) Qual é o resultado da multiplicação na ficha verde?
b) Qual é o resultado da multiplicação na ficha vermelha?
c) Efetuando a subtração entre os resultados da ficha vermelha e o resultado da ficha verde, qual número vamos obter?
Tabuada do 2
AS TABELAS DE MULTIPLICAÇÃO
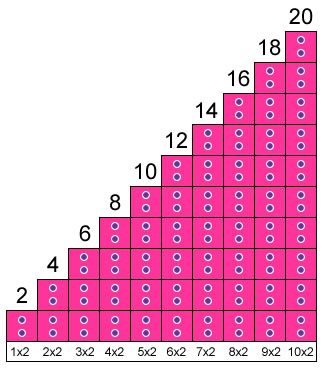
Agora, é você que vai completar:
| a) 1 vezes 2 é igual a | f) 6 vezes 2 é igual a |
| b) 2 vezes 2 é igual a | g) 7 vezes 2 é igual a |
| c) 3 vezes 2 é igual a | h) 8 vezes 2 é igual a |
| d) 4 vezes 2 é igual a | i) 9 vezes 2 é igual a |
| e) 5 vezes 2 é igual a | j) 10 vezes 2 é igual a |
| a) x 2 = 0 | f) x 2 = 18 |
| b) x 2 = 8 | g) x 2 = 20 |
| c) x 2 = 14 | h) x 2 = 2 |
| d) x 2 = 16 | i) x 2 = 10 |
| e) x 2 = 12 | j) x 2 = 4 |
3) Vamos colocar o sinal de + ou de x, de acordo com o resultado
| a)2 1 = 2 | g) 2 5= 7 |
| b) 2 5 = 10 | h) 2 1= 3 |
| c) 2 9= 11 | i) 2 4= 8 |
| d) 2 6= 8 | j) 2 3= 6 |
| e) 2 7= 9 | l) 2 8= 10 |
| f) 2 7= 14 | m) 2 3= 5 |
4) Você tem as seguintes fichas numeradas:
2
|
4
|
6
|
8
|
10
|
12
|
14
|
16
|
18
|
Quais delas você usaria para dar o resultado correto das multiplicações a seguir?
a) 3 x 2
b) 2 x 2
c) 8 x 2
d) 5 x 2
e) 1 x 2
f) 9 x 2
Tabuada do 5
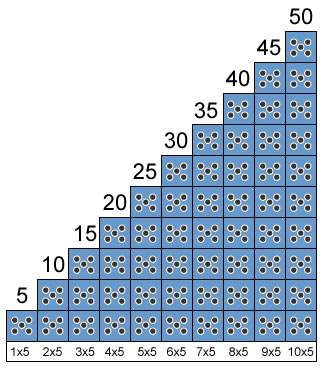
Agora complete:
a) 1 vezes 5 é igual a
b) 2 vezes 5 é igual a
c) 3 vezes 5 é igual a
d) 4 vezes 5 é igual a
e) 5 vezes 5 é igual a
f) 6 vezes 5 é igual a
g) 7 vezes 5 é igual a
h) 8 vezes 5 é igual a
i) 9 vezes 5 é igual a
j) 10 vezes 5 é igual a
2)Descubra o número que está faltando e complete:
| a) x 5 = 50 | f) x 5 = 15 |
| b) x 5 = 5 | g) x 5 = 35 |
| c) x 5 = 45 | h) x 5 = 20 |
| d) x 5 = 10 | i) x 5 = 30 |
| e) x 5 = 40 | j) x 5 = 25 |
3- Coloque o sinal de + ou de x:
| a) 5 2 = 10 | f) 5 3 = 15 |
| b) 5 3 = 8 | g) 5 8 = 13 |
| c) 5 9 = 14 | h) 5 1 = 6 |
| d) 5 5 = 25 | i) 5 4 = 20 |
| e) 5 7 = 35 | j) 5 7 = 12 |
| l) 5 2 = 7 | m) 5 1 = 5 |
4- Observe as fichas numeradas:
15
|
20
|
30
|
95
|
5
|
a) 5 x 6
b) 5 x 3
c) 5 x 4
d) 5 x 1
Atividades de multiplicação
ATIVIDADES
1) Agora Complete:
| • Edu desenhou 2 grupos de 4 bolas: 2 vezes 4 bolas são bolas 2 x 4 = |  |
| • Edu desenhou 3 grupos de 4 bolas: 3 vezes 4 bolas são bolas 3 x 4 = |  |
| • Edu desenhou 4 grupos de 4 bolas: 4 vezes 4 bolas são bolas 4 x 4 = |  |
2) Observando as figuras, complete:
| a) 3 vezes 2 flores, são flores. 3 x 2 = |  |
| b) 2 vezes 4 triângulos, são triângulos 2 x 4 = |  |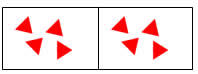
| c) 3 vezes 6 bolas, são bolas 6 x 3 = |  |
| d) 4 vezes 3 aviões, são aviões 4 x 3 = |  |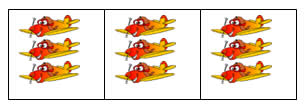
| e) 2 vezes 6 palitos, são palitos 2 x 6 = |  |
| f) 3 vezes 5 bombons são bombons 3 x 5 = |  |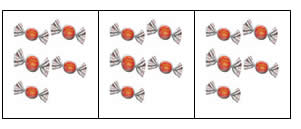
| g) 4 vezes 9 bandeirinhas, são bandeiras 4 x 9 = |  |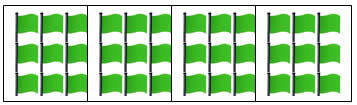
Tabuada do 4
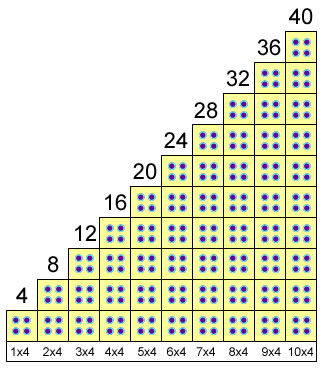
Agora Complete:
a) 1 vezes 4 é igual a
b) 2 vezes 4 é igual
c) 3 vezes 4 é igual a
d) 4 vezes 4 é igual a
e) 5 vezes 4 é igual a
f) 6 vezes 4 é igual a
g) 7 vezes 4 é igual a
h) 8 vezes 4 é igual a
i) 9 vezes 4 é igual a
j) 10 vezes 4 é igual a
2) Vamos Completar?
a) x 4 = 32
b) x 4 = 12
c) x 4 = 28
d) x 4 = 4
e) x 4 = 24
f) x 4 = 8
h) x 4 = 16
i) x 4 = 40
j) x 4 = 36
3) Coloque o sinal de + ou de x:
a) 4 6 = 10
b) 4) 2 = 8
c) 4 9 = 36
d) 4 5 = 9
e) 4 3 = 12
f) 4 8 = 12
g) 4 3 = 7
h) 4 1 = 5
i) 4 5 = 20
j) 4 4 = 16
l) 4 6 = 24
m) 4 4 = 8
4) Observe as multiplicações indicadas a seguir:
4 x 3
|
4 x 6
|
a) Qual é o resultado da multiplicação na ficha verde?
b)Qual é o resultado da multiplicação na ficha vermelha?
c)Adicionando os 2 resultados, que número você vai encontrar?
ESPECIAL TABUADA - PARTE 3
MANEIRAS DIFERENTES DE APRENDER A TABUADA
Antigamente era de extrema importância saber a tabuada “na ponta da língua”, não que hoje em dia não seja importante saber toda ela. A diferença é que os métodos que são utilizados para que o aluno aprenda a tabuada é que são diferentes.
A repetição, a prática cotidiana de uma atividade com certeza é uma das maneiras mais viáveis de se aprender algo, mas essa repetição deve ter contexto, o simples fato de ficar repetindo até decorar não quer dizer que estará aprendendo, o máximo que ocorrerá é o famoso “decoreba”. Essa é a forma que as pessoas acham que se deve estudar a tabuada. Acredita-se que não tem como aprender a tabuada, apenas decorá-la.
A tabuada nada mais é que operações de multiplicação que parte da operação de adição de parcelas iguais. Por exemplo: 5 + 5 + 5 + 5 + 5 + 5, a soma pode ser representada pela multiplicação, ou seja, é a soma de 6 parcelas iguais, portanto 5 + 5 + 5 + 5 + 5 + 5 é o mesmo que 5 x 6 = 30.
Podemos partir dessa idéia para compreender toda a tabuada, ou ainda utilizar de algumas estratégias como o jogo.
Existem inúmeros jogos, alguns adaptados para a tabuada, outros criados especificamente para essa situação. Dentre eles destacam-se:
Bingo matemático
Batalha Naval
Jogo da memória
Jogos: Batalha numérica
Jogo do repartir
Jogos de Dados
Dedo no gatilho
Labirinto
Dominó
Esses jogos facilitam a aprendizagem, mostram um lado divertido de estudar a tabuada. São atividades que podem ser praticadas diariamente em sala de aula ou até mesmo em casa com os pais.
A repetição, a prática cotidiana de uma atividade com certeza é uma das maneiras mais viáveis de se aprender algo, mas essa repetição deve ter contexto, o simples fato de ficar repetindo até decorar não quer dizer que estará aprendendo, o máximo que ocorrerá é o famoso “decoreba”. Essa é a forma que as pessoas acham que se deve estudar a tabuada. Acredita-se que não tem como aprender a tabuada, apenas decorá-la.
A tabuada nada mais é que operações de multiplicação que parte da operação de adição de parcelas iguais. Por exemplo: 5 + 5 + 5 + 5 + 5 + 5, a soma pode ser representada pela multiplicação, ou seja, é a soma de 6 parcelas iguais, portanto 5 + 5 + 5 + 5 + 5 + 5 é o mesmo que 5 x 6 = 30.
Podemos partir dessa idéia para compreender toda a tabuada, ou ainda utilizar de algumas estratégias como o jogo.
Existem inúmeros jogos, alguns adaptados para a tabuada, outros criados especificamente para essa situação. Dentre eles destacam-se:
Bingo matemático
Batalha Naval
Jogo da memória
Jogos: Batalha numérica
Jogo do repartir
Jogos de Dados
Dedo no gatilho
Labirinto
Dominó
Esses jogos facilitam a aprendizagem, mostram um lado divertido de estudar a tabuada. São atividades que podem ser praticadas diariamente em sala de aula ou até mesmo em casa com os pais.
Atividades Tabuada - Ultima Parte
Um pouco de história ajuda a entender a dúvida
Na escola de trinta anos atrás, saber a tabuada de cor, "na ponta da língua", era ponto de honra para alunos e professores do antigo primário. Poucas pessoas, talvez, ousassem por em dúvida a necessidade desta mecanização.
Na década de 60 despontaram movimentos de todos os tipos, rompendo com tradições seculares: o feminismo, a revolução sexual, os hippies, os Beatles, a revolução cultural na China, as passeatas de estudantes em Paris-68 etc. O ensino da matemática não ficou indiferente ao clima revolucionário. A Matemática Moderna modificou o ensino da matemática. Não vamos discutir aqui as características deste movimento mas, dentre seus aspectos positivos, destacava-se o desejo de aprendizagem com compreensão.
No conjunto de críticas ao ensino tradicional, uma recaiu sobre a mecanização da tabuada. Diversas escolas aboliram e proibiram a memorização da mesma. A professora ou professor que obrigasse seus alunos a decorar a tabuada era, muitas vezes, considerado "antiquado", "retrógrado".
O argumento dos renovadores, contrário á memorização, era basicamente este: "não se deve obrigar o aluno a decorar a tabuada; deve-se, isto sim, criar condições para que ele a compreenda". Os adeptos das novas tendências alegavam que, se o aluno compreendesse a tabuada, se ele entendesse o significado de códigos como 3 x 7, 8 x 6, 5 x 9 etc., então, quando precisasse, sozinho, pensando, ele descobriria os resultados.
Alguns professores rebatiam esta afirmação alegando que, sem saber a tabuada de cor, um aluno não poderia realizar multiplicações e divisões. A cada momento, na realização de cálculos e na resolução de problemas ele "engasgaria" por não saber a tabuada de cor.
É curioso observar que, passados estes anos todos, esta discussão pemanece entre nós.
É necessário compreender
Nesta discussão, apesar das divergências, há uma opinião unânime: deve-se condenar a mecanização pura e simples da tabuada. É absurdo exigir que os alunos recitem: "dois vezes um, dois; dois vezes dois, quatro;...", sem que eles entendam o significado do que estão dizendo. A multiplicação (bem como todas as outras operações e a noção de número e o sistema de numeração decimal) precisa ser construída e compreendida. Esta construção é o resultado de um trabalho mental por parte do aluno.
O termo tabuada é bastante antigo e designa um conjunto de fatos, como por exemplo:
3 x 1 = 3, 3 x 2 = 6, 3 x 3 = 9, etc.
3 x 1 = 3, 3 x 2 = 6, 3 x 3 = 9, etc.
Esses fatos têm sido chamados, por diversos autores, de fatos fundamentais da multiplicação.
Trabalhando com materiais variados (papel quadriculado, grãos, palitos), explorando jogos e situações diversas (quantos alunos serão necessários para formar 4 times de vôlei?), os alunos poderão, aos poucos, construir e registrar os fatos fundamentais que compõem a tabuada.
Construindo a tabuada
A atividade que vamos descrever é bastante rica. Nela, os alunos constróem a tabuada, partindo de alguns fatos simples já trabalhados anteriormente. Primeiramente organizamos a tabela e registramos com os alunos os fatos já conhecidos (até 5 x 5).
É fácil completar a primeira linha pois ela se refere á multiplicação por 1. Também é fácil completar a primeira coluna
Proponha aos alunos que descubram quanto dá, por exemplo, 8 x 3. Eles podem obter este resultado, por exemplo, através de adições sucessivas:
MAS PODEM TAMBÉM OBTER 8 X 3 DE OUTRO MODO. COMO 8 = 5 + 3, PODEM PERCEBER QUE:
8 x 3 = 5 x 3 + 3 x 3
NA TABELA TEMOS OS VALORES DE 5 X 3 E 3 X 3, LOGO:
8 x 3 = 15 + 9 = 24
DA MESMA FORMA PODEM FAZER:
9 x 3 = 5 x 3 + 4 x 3 = 15 + 12 = 27
7 x 4 = 3 x 4 + 4 x 4 = 12 + 16 = 28
Os produtos obtidos vão sendo registrados na tabela.
Nessa altura do trabalho com a multiplicação os alunos já terão percebido que 3 x 5 = 5 x 3, 2 x 4 = 4 x 2, etc. Assim, como já descobriram que 8 x 3 = 24, concluem que 3 x 8 = 24; como 9 x 3 = 27, então 3 x 9 = 27. E a tabela vai sendo completada.
Note que nesta construção, vão sendo usadas intuitivamente, diversas propriedades da multiplicação. Ao longo desta atividade a compreensão da multiplicação está presente o tempo todo.
Uma vez completada a tabela, podemos prosseguir explorando-a ainda mais:
A linha do 1 é igual á coluna do 1. A linha do 2 é igual á coluna do 2 etc. Isto ocorre porque 3 x 1 = 1 x 3, 2 x 4 = 4 x 2 etc.
Na linha do 1 (e na coluna do 1) os números aumentam de 1 em 1.
Na linha 2 (e na coluna do 2) os números aumentam de 2 em 2.
E assim por diante. Na linha 9 (e na coluna do 9) os números aumentam de 9 em 9. É fundamental explorar este ritmo, esta regularidade da tabuada.
Peça aos alunos que localizem todos os 12 da tabela. Ele aparece quatro vezes. Estas quatro aparições correspondem aos produtos 3 x 4, 4 x 3, 2 x 6 e 6 x 2. Faça o mesmo com outros números, com 16, 15 etc. Uns aparecem três vezes, outros duas e outros ainda só uma vez.
A memorização também é necessária
É importante que, uma vez compreendidos os fatos fundamentais, eles sejam, aos poucos, memorizados pelas crianças. Para isso é interessante utilizar jogos variados. Vamos dar um exemplo.
O tabuleiro do desenho, com 36 casinhas, pode ser desenhado em cartolina ou qualquer outro papel. Os números que nele aparecem são os resultados das multiplicações de
1, 2, 3, 4, 5 e 6 por 1, 2, 3, 4, 5 e 6:
5 x 6 = 30, 1 x 2 = 2, 3 x 3 = 9, 4 x 6 = 24 etc.
1, 2, 3, 4, 5 e 6 por 1, 2, 3, 4, 5 e 6:
5 x 6 = 30, 1 x 2 = 2, 3 x 3 = 9, 4 x 6 = 24 etc.
Para jogar são necessários dois dados.
Um aluno joga contra outro. Na sua vez, cada jogador lança os dois dados, observa os dois números obtidos e procura, no tabuleiro, o produto dos mesmos, aí colocando um grão de feijão, por exemplo. O outro jogador deve assinalar seus resultados com outra marca, como tampinhas por exemplo.
Vence o jogador que tiver 3 marcadores numa mesma linha, coluna ou diagonal.
O professor pode ainda promover com os alunos a "gincana da multiplicação", em que um grupo faz perguntas a outro: "quanto é 3 x 9?". Ou então um grupo diz o produto (por exemplo: 63) e o outro encontra os fatores (7 e 9).
Estas atividades contribuem para a memorização da tabuada. É claro que este esforço de memorização não deve ser obsessivo. Se um aluno, em algum momento, não se lembrar, por exemplo, de quanto é 7 x 8, é importante que ele tenha a chance de pensar e descobrir por si próprio. Além disso, devemos discutir com os alunos a necessidade desta memorização. Eles devem saber que ela é necessária para que possamos apresentar um bom desempenho em situações mais complexas. A necessidade da memorização justifica-se. Não é á toa que os fatos fundamentais têm este nome. A fixação dos mesmos é importante para que o aluno compreenda e domine algumas técnicas de cálculo. Na exploração de novas idéias matemáticas (frações, geometria, múltiplos, divisores etc) a multiplicação aparecerá com freqüência. Se a criança não tiver fixado os fatos fundamentais, a cada momento ela engasgará na tabuada, desviando sua atenção das novas idéias que estão sendo trabalhadas.
Respondendo então á pergunta que dá título a esta leitura, devemos dizer que o aluno não deve decorar mecanicamente a tabuada, mas que precisa fazer um certo esforço para memorizar. Insistimos porém que esta memorização deve ser precedida pela compreensão. A ênfase do trabalho deve ser posta na construção dos conceitos. A preocupação com a memorização não deve ser obsessiva e exagerada.
http://suzettepaula.blogspot.com/2008/11/tabuadas-de-multiplicao.html E http://mundinhoencantadoprofe.blogspot.com/2009/11/atividades-para-aprender-tabuada.html
Olá amiga Educadora Ana,
ResponderExcluirAdorei seu blog riquíssimo de detalhes,tenho certeza qualquer educador que passar por aqui terá um excelente material para trabalhar com seus alunos.Parabéns.Abraços tenha uma maravilhosa Páscoa.